Contrairement à ce qu'on a pu dire autrefois, l'apport du monde arabe dans la mathématisation et la représentation du monde est très importante. Les savants arabes développèrent et améliorèrent l'astrolabe qu'ils utilisèrent non seulement pour des relevés astronomiques mais aussi dans les mesures terrestres. Ces instruments d'un autre temps qui furent indispensables en navigation et en astronomie, furent beaucoup utilisés dans le monde arabe qui avait besoin, de par sa religion, de déterminer l'heure des prières, la direction de la Mèque, les dates de fêtes religieuses variables en fonction du mouvement des astres. Ils ne sont plus utilisés mais restent de merveilleuses oeuvres d'art pour certains d'entre eux. Le musée des sciences d'Oxford en propose de magnifiques très bien photographiés. Oxford
Pour avoir une description de son fonctionnement : Voir.
Superbe instrument : origine, Google images.
L'astrolabe est un instrument beaucoup plus compliqué que ceux dont nous avons déjà parlé sur ce blog.
Le musée des sciences de Florence nous propose une belle vidéo qui retrace son histoire simplifiée très instructive, en italien, hélas, mais accessible me semble-t-il.
La vidéo.
Le lien suivant vous mènera à une histoire un peu plus détaillée de l'astrolabe. Les propos précédents comme ceux du site de Philippe Dutarte illustrent bien ce qui est dit dans la présentation du blog sur les déplacements des centres de connaissance, en particulier autour du bassin méditerrannéen.
Vers le site de P. Dutarte consacré aux instruments anciens.
Vous pouvez aussi comparer avec ce qu'en dit wikipedia qui cite d'ailleurs dans ses sources Philipe Dutarte.
Wikipedia.
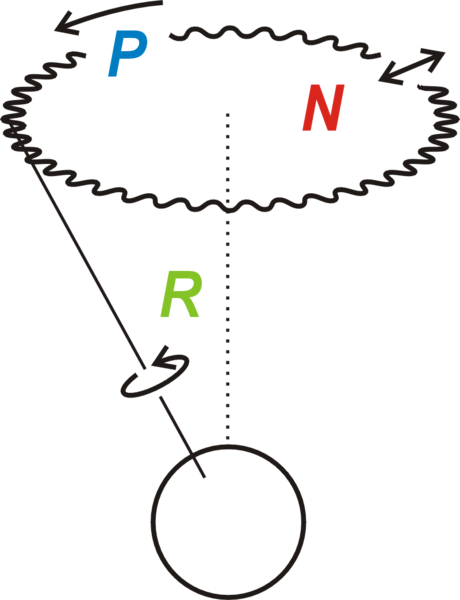
D'après G. SINOUE, dans "Avicenne", livre qui relate la vie de ce célèbre médecin et scientifique, Al Biruni aurait fait la mesure de ce rayon et aurait obtenu 6338,80km, valeur vraiment proche de celle que nous lui attribuons aujourd'hui ( 6353,41km à la latitude de Nandana ). Mais il confesse aussi des échecs sur ce sujet. Qu'en est-il vraiment ? ... La méthode utilisée reposerait sur la mesure de la hauteur d'une montagne, à partir du sommet de laquelle on mesure les angles de la verticale avec la tangente à l'horizon.
Cliquer sur l’image pour lire le texte.
Pour en savoir plus sur Al Biruni, le site de Serge Mehl : Voir
Vous verrez alors que ce fut un grand savant du moyen âge très en avance sur ce que nous faisions à la même époque en Europe, en particulier en ce qui concerne la trigonométrie qui ne se développera vraiment qu'avec Regiomontanus(1436-1476).
Le site de l'académie de St Andrews qui fait la biographie de nombreux savants, confirme qu'il obteint au XIe siècle le rayon de la terre avec une précision qui ne sera pas atteinte en occident avant le XVIe siècle.
"Important contributions to geodesy and geography were also made by al-Biruni. He introduced techniques to measure the earth and distances on it using triangulation. He found the radius of the earth to be 6339.6 km, a value not obtained in the West until the 16th century. His Masudic canon contains a table giving the coordinates of six hundred places, almost all of which he had direct knowledge."
Voir plus. (en anglais)
Pour une connaissance plus approfondie des apports du monde arabe, voir cette belle page qui retrace l'histoire de l'astronomie de l'antiquité au XVè siècle. Ici
Ci-dessous, second observatoire connu au monde qui fut érigé à Samarcande par le prince Ulugh Beg (1393-1449). C'est l'astronome et mathématicien al-Kashi (mort en 1429) qui y dirige les travaux. (extrait de cette même page web)





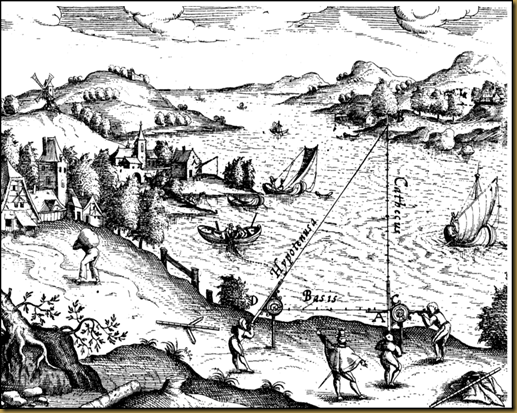















 On peut voir de belles illustrations de son utilisation dans le livre de Frisius(Gemma Frison), la cosmographie de Pierre Apian, que vous pouvez consulter sur le site anglais qui commente toutes les pages.
On peut voir de belles illustrations de son utilisation dans le livre de Frisius(Gemma Frison), la cosmographie de Pierre Apian, que vous pouvez consulter sur le site anglais qui commente toutes les pages.






















 Ci-dessus, un zoom sur un des cartons formant cette carte qui représente les landes où l'on voit qu'il n'y a pas de triangles, la région marécageuse à l'époque ne se prêtant pas à ce type de relevé.
Ci-dessus, un zoom sur un des cartons formant cette carte qui représente les landes où l'on voit qu'il n'y a pas de triangles, la région marécageuse à l'époque ne se prêtant pas à ce type de relevé. 